GEPS: Boosting Generalization in Parametric PDE Neural Solvers through Adaptive Conditioning

Armand Kassaï Koupaï1, Jorge Mifsut-Benet1, Yuan Yin2, Jean-Noël Vittaut3, Patrick Gallinari1,4
1Sorbonne Université ISIR, 2Valeo.ai, 3Sorbonne Université LIP6, 4Criteo AI Lab
NeurIPS 2024
Paper Code arXiv
Teaser Image

The chosen multi-environment setting for GEPS for the Kolmogorov PDE. GEPS leverages information from multiple environments, each environment defined by specif PDE parameter values, to boost generalization in parametric PDEs neural solvers.

Abstract

Solving parametric partial differential equations (PDEs) presents significant challenges for data-driven methods due to the sensitivity of spatio-temporal dynamics to variations in PDE parameters. Machine learning approaches often struggle to capture this variability. To address this, data-driven approaches learn parametric PDEs by sampling a very large variety of trajectories with varying PDE parameters. We first show that incorporating conditioning mechanisms for learning parametric PDEs is essential and that among them, \textit{adaptive conditioning}, allows stronger generalization. As existing adaptive conditioning methods do not scale well with respect to the number of PDE parameters, we propose GEPS, a simple adaptation mechanism to boost GEneralization in Pde Solvers via a first-order optimization and low-rank rapid adaptation of a small set of context parameters. We demonstrate the versatility of our approach for both fully data-driven and for physics-aware neural solvers. Validation performed on a whole range of spatio-temporal forecasting problems demonstrates excellent performance for generalizing to unseen conditions including initial conditions, PDE coefficients, forcing terms and solution domain.

Motivating the adaptive conditioning approach

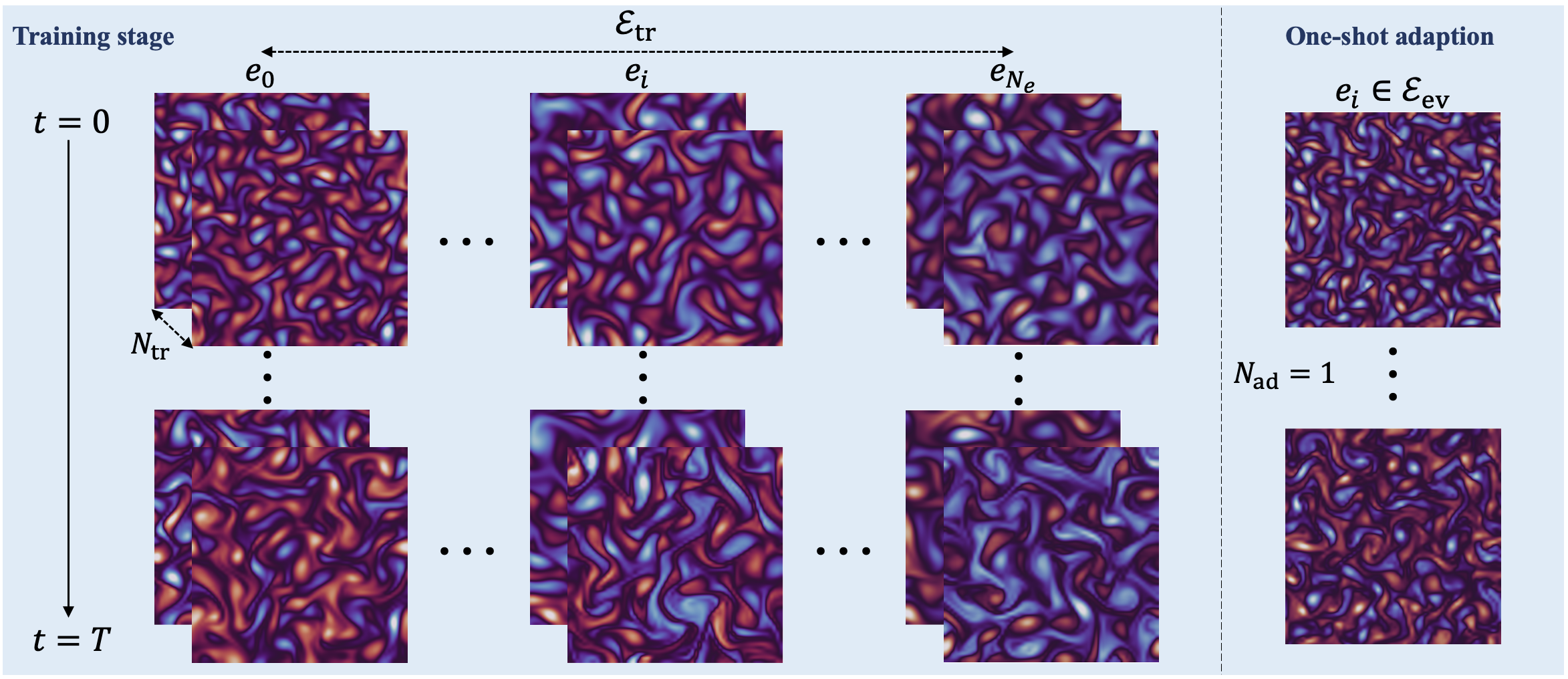
One goal of this paper is to demonstrate the relevance of a multi-environment setting, compared to a more traditional ERM method, which advocate the use of large datasets to boost generalization. We thus compare it with an ERM approach when scaling the number of training trajectories and environments. The models are trained on a range of environments - corresponding to different coefficients of the underlying PDE - and evaluated on the same environments with different initial conditions.

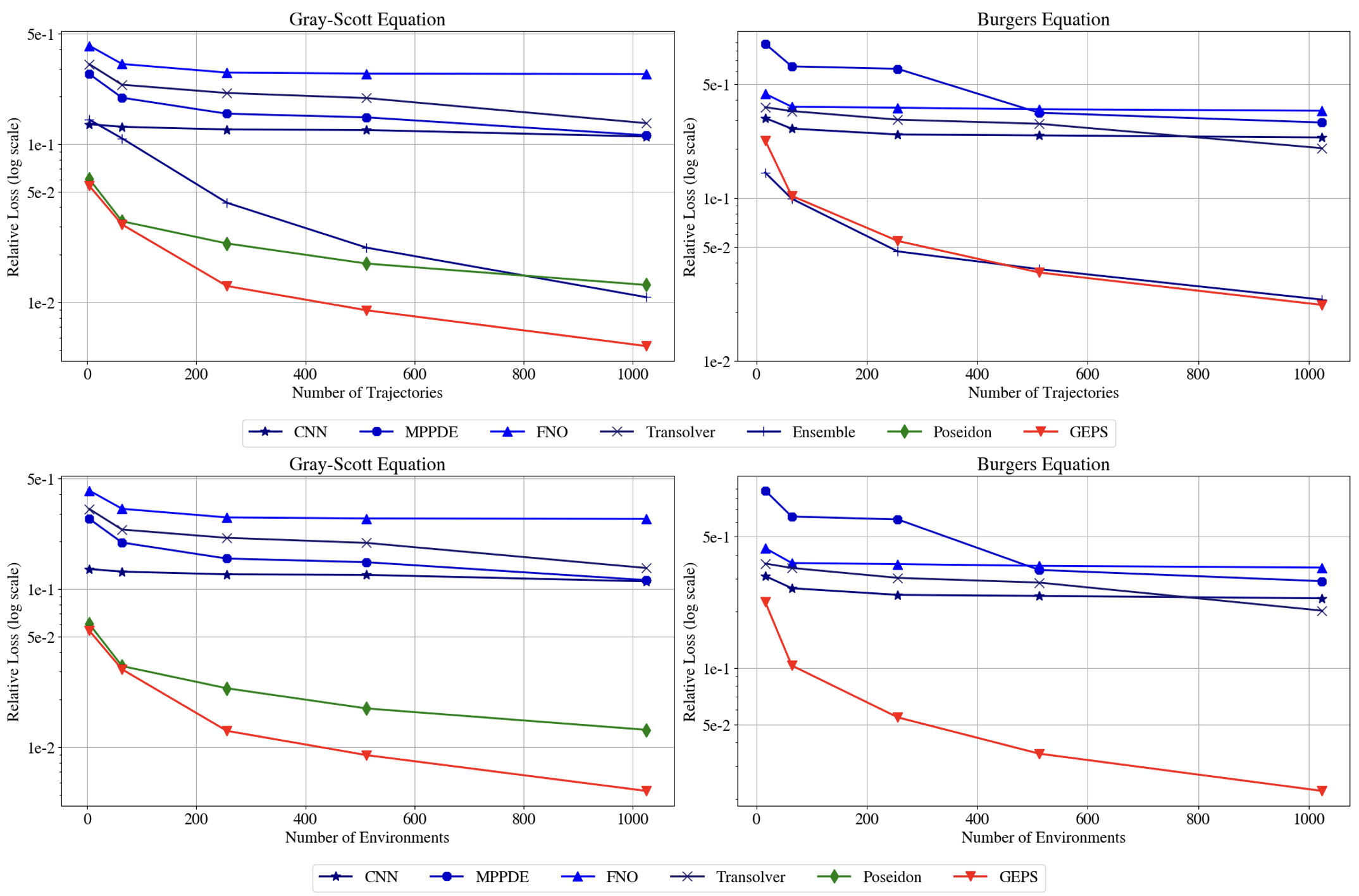
key observation

Comparison of ERM methods approaches (shades of blue) and Poseidon (green) with our adaptive conditioning approach GEPS (red). We evaluate the performance of different methods when increasing the number of training trajectories (at the top) and when increasing the number of environements (at the bottom) for two PDE equations: Gray-Scott (left) and Burgers (right).


We experimentally show that traditional ERM methods fail to capture the diversity of behaviors and their performance stagnate when increasing the number of training trajectories per environments and environments. Poseidon is able to capture such diversity, but its performance is lower compared to GEPS while pretrained on very large datasets. GEPS benefits from being trained on a large amounts of environments and training trajectories, as its performance scale respectively with the number of trajectories and environements.

GEPS framework

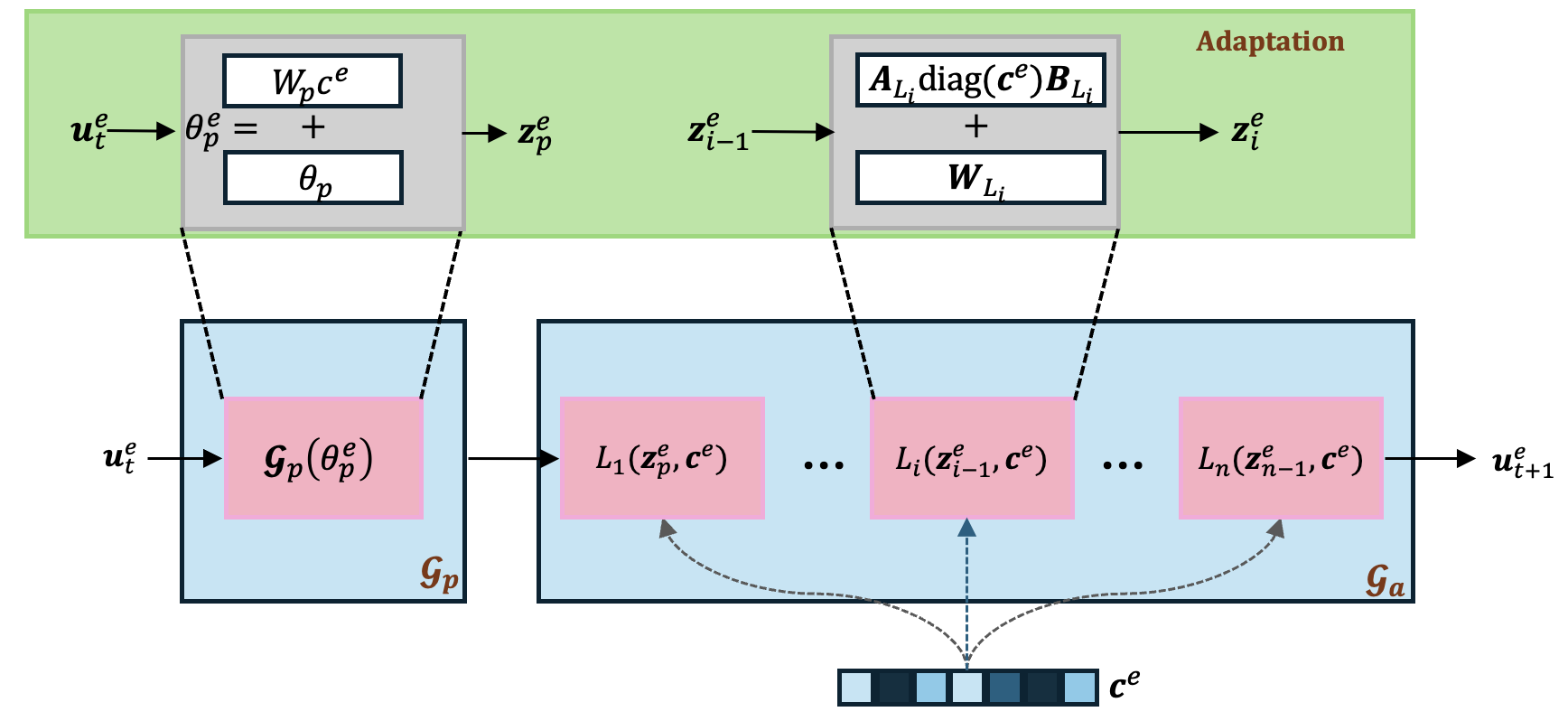
We introduce our framework for learning to adapt neural PDE solvers to unseen environments. It leverages a 1st order adaptation rule for low-rank and rapid adaptation to a new PDE instance. We consider two common settings for learning PDE solvers; the first one leverages pure data-driven approaches and the second leverages priors information for learning hybrid neural PDE solvers.

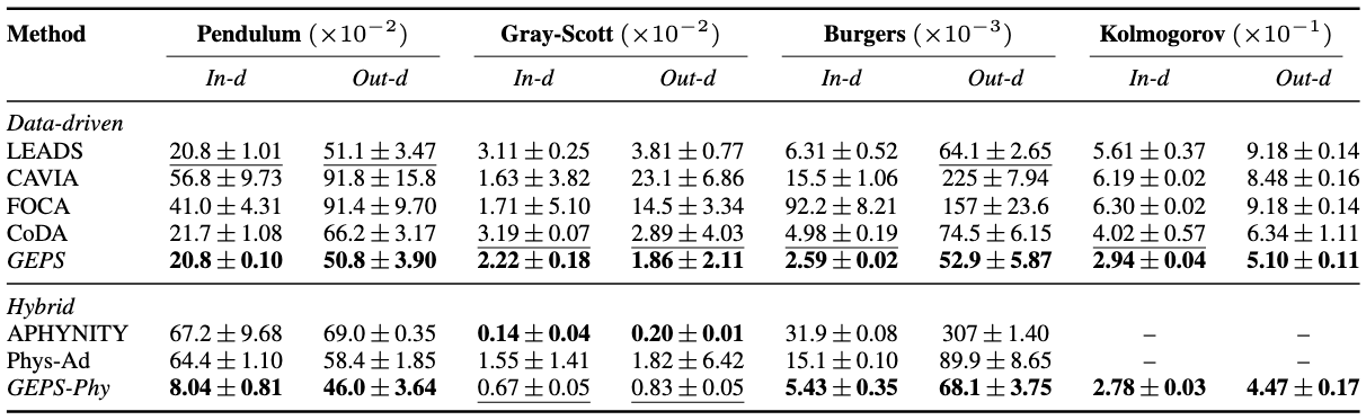
key observation

Our adaptation framework for for a hybrid model. For the agnostic model, the physics component (bottom left) is removed. Blocks in blue refer to the physical (bottom left) and data-driven (bottom right) modules. Blocks in pink refer to the trainable modules. The green block describes the adaptation mechanism for the physical (top left) and data-driven (top right) component. ce is the context used to adapt the two components.


Results

We provide quantitative results of our methods compared to other adaptive conditioning approaches.

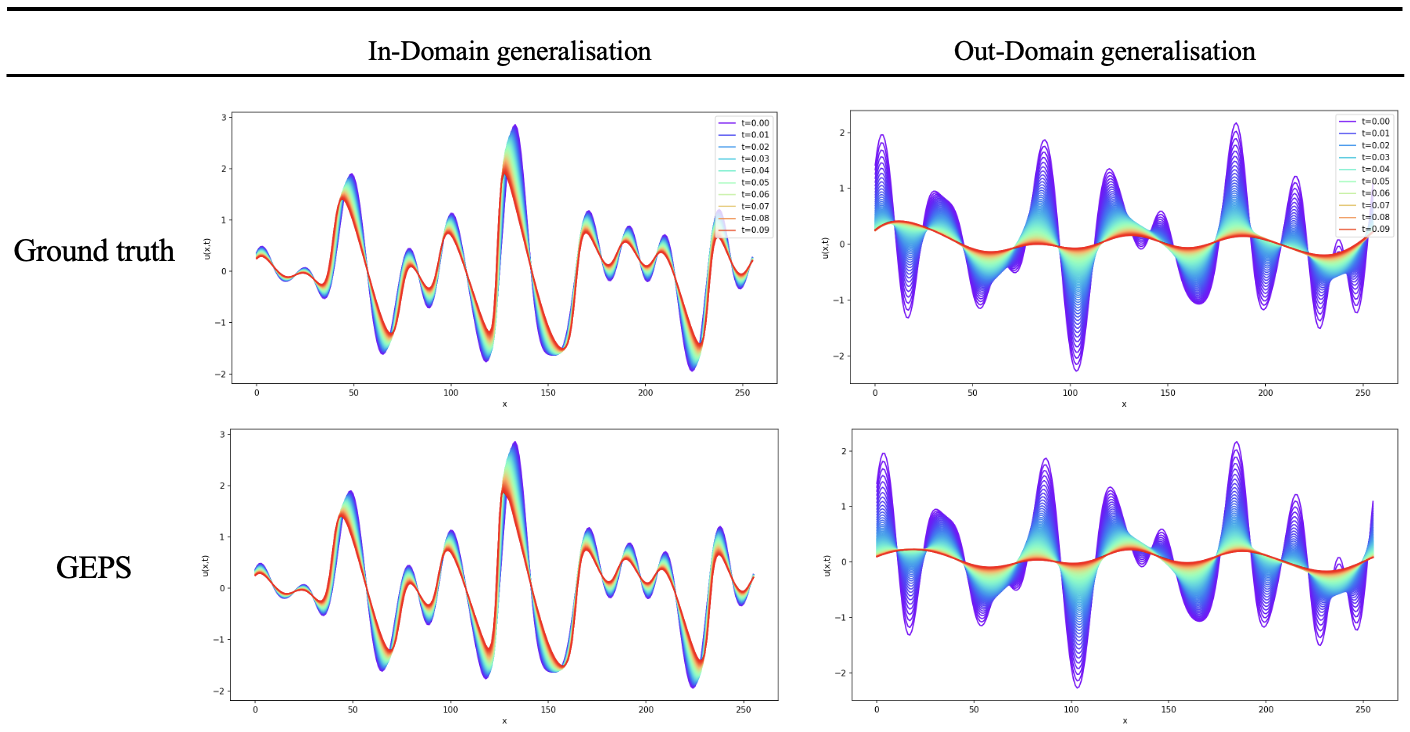
key observation

In-distribution and Out-distribution results on 32 new test trajectories per environment. For out-distribution, models are fine-tuned on 1 trajectory per environment. Metric is the relative L2. '--' indicates inference has diverged.


We provide qualtitative results for the Burgers equation. For more details, please refer to our paper.

key observation

BibTeX

@article{kassai2024geps,
  title={GEPS: Boosting Generalization in Parametric PDE Neural Solvers through Adaptive Conditioning},
  author={Kassaï Koupaï, Armand and Mifsut Benet, Jorge and Vittaut, Jean-Noël and Gallinari, Patrick},
  journal={38th Conference on Neural Information Processing Systems (NeurIPS 2024)},
  year={2024}
  }